GUIDELINES
Name-codes, Nametags, Number-codes, Number-tags
The ABZZ system can be used prospectively to generate a new number-code from words which have special meanings to the user. It can also be used retrospectively to generate a name-code for any given number, short or long.
Prospective nametags
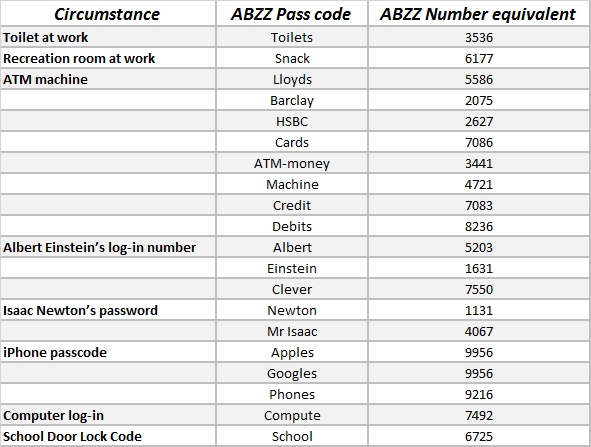
The ABZZ nametag system is excellent when it comes to generating new memorable numbers. In self- generated memorable numbers, it is better to generate the numbers from our own words; words which are meaningful and memorable to us. For instance, you may desire to generate a new pass-code for the combination lock of the “Coffee Room” in your workplace.
The desire is to generate a number which is easily remembered by all the office workers who use the coffee room. The memorable number could be encoded as “coffee room” (74404). You might also encode it in the word “Nescafe” (1674). Another prospective example of using the ABZZ is changing your pin number at the ATM machine.
If your name is Casper, you can change your password to “7690”. For self- generated memorable numbers, it is advisable to use the prospective method and the number of available words you can use is only limited by your vocabulary. The table below shows a few examples of using the prospective method to create word codes:
Retrospective Use of ABZZ nametags
Externally generated memory numbers are usually made up by others and given to us to use. This is usually the case with access codes, telephone numbers, and registration numbers. In these cases, you may need to generate your own word-codes or check the word-code decoder to find the word equivalents of your memorable numbers. This ABZZ decoder displays word-codes for all the numbers ranging from “0” to “9999”.
As a sequel to this publication, it is intended to publish online a thesaurus of all the numbers of up to 10 digits and their lists of word-codes using universally understood vocabulary.
Some numbers in the ABZZ thesaurus have only a few word code options, but other numbers could have word code options reaching several hundreds. This is good and gives people the choice to choose words most appealing to them.
It is up to the user to choose which of these word codes has a meaning to him. If you live in England, the compound word “Hang-hoe” for 2192 would make more meaning whereas the word “Huang-He” would be preferable in China.
For a medical doctor, the word “Nocturia” for 1730 would be more attractive whereas a lawyer is more likely to prefer the word “Enactor”.
Alpha-numeric memorable codes; Storing and Concealing Passwords
The ABZZ system allows for generation of very strong alpha-numeric passwords which are unique to us. Using the ABZZ coding system a person named Daffy Duck could write his pass-code as “daffy877”, or “844duck”. Different variations of this could be generated using the same basic technique.
You can also partially convert number digits into ABZZ. Given a phone number like 0800250008, you can remember it by partially changing it to ABZZ. In this case 0800250008 could then become 0800Blizzard where Blizzard represents the 250008 component of the number.
You can decide on a new password called “Open Sesame” which in alpha-numeric format can become “Open664”.
You can also use the ABZZ to code and conceal pin numbers. Tear the original pin number given to you by the bank and save the number as an ABZZ word-code in a diary or other book. The word-code can be buried among other words in a sentence or alphabet soup.
You don’t necessarily even have to remember the name-code. You just write the name code in a place of choice and anytime you look it up, you convert it back to numbers.
Sentence Option variations in the ABZZ system
One variant use of the ABZZ is to utilise only the numbers encoded by the first consonant in every word of a sentence, catch-phrase, quotation, song, poem or other verse. The following quotations are examples: “Life is too short to be little”; the initial consonants of each word are LSTSTBL or number-code equivalent of 5636325.
“A book is a machine to think with”; the initial consonants are BSMTTW or number-code equivalent of 264331. These numbers could well be somebody’s memorable codes. Similarly, one may decide to use only the last consonant in each word.
In the catch phrase “repeal the law of gravity”, the last consonants of each word will form “LHWT” or number-code equivalent of 5213.
Abbreviations
Every consonant in a word code counts. Familiar abbreviations, titles, acronyms and initials of names could all be used to complement words. For instance “CT scanner” would have number-code equivalent of 7367110; “BT.com” would be 2374; Mini.co.uk would be 4177, and “Mr DJ Sidebottom” would be 4088682334.
Chunking and creating known or new compound words
The working memory of man is known to have a limited capacity. A common measure of the working memory is the memory span, which is said to have around seven elements (plus or minus two). These elements are called chunks. A memory element or chunk could be made of digits, letters, words or other verbal contents.
The number of elements in a normal memory span is said to be around 7 for digits, 6 for letters and 5 for words. The number of elements or chunks in a memory span is said to depend on the category and characteristic of the chunks used. A number with 7 digits will thus have 7 chunks. Numbers with more than 9 digits or chunks are difficult to remember off-hand unless a memory technique is used either knowingly or unknowingly.
A number composed of 3 digits is easier to remember than a number composed of 7 digits. For words, the memory span is longer when the words are short and more familiar. With or without explicit knowledge of how this system operates, humans have instinctively learnt to increase their memory span by organising memory items into easily remembered chunks.
Using the ABZZ system, a single word chunk can be used to code multiple number digit chunks e.g. the single word chunk ‘childishness’ would code the number ‘725862166’ which is composed of 9 digit chunks.
Most numbers below 100,000 will have single word code equivalents. When single word codes cannot be found for a long multi-digit number, it is advisable to break the number into batches of 1- 4 digits that can easily be coded using 2, 3 or 4 consonant words. The word codes for the number- batches are then combined to form meaningful compound words or phrases. As an example, there may not be an easily available meaningful simple word code for the number 2469.
You can form a new compound word such as “bum-sag” to code for 2469; the first 2 digits will form “bum” and the last two will form “sag”. It is not difficult to imagine the meaning of the new compound word “bum-sag”. As an alternative, you can also form the compound word “beef-soup” which also codes for the same number.
Precision in spellings
Numbers are digital and very precise. Word spellings can be altered without changing the meaning of a word. But numbers or number groups cannot be altered without changing what the number stands for. Changing the vowel component of a word does not change the number equivalent; but any change in the consonant component of a word changes its number equivalent.
The implication of this is that when converting numbers to words, we have to be precise about the spelling we have in mind. The ABZZ number equivalent of a word depends strictly on the letters that form the word and not the sound of the word. It is important to remember which spelling you have used when words having the same meaning can be spelt in different ways e.g. jail/gaol, hiccough/hiccup, cosy/cozy, Odesa/Odessa, enrol/enroll. It may be important in some cases to be clear whether you are using British spellings or American spellings.
The words polarize and polarise have the same meaning but they are spelt differently by the Americans and the British. If you spell the word polarize, the number-code equivalent would be 9500; but if spelt as polarise, the number-code equivalent changes to 9506.
The sound may be similar, but the spellings, meanings and the number equivalents may be very different. In the ABZZ word code system, there is a huge difference between “gracias” and “grassy ass”. The number equivalents are 9076 and 906666. It should be remembered that words may even have the same alphabets but have differing meanings e.g. capsize and cap-size; kidnap and kid-nap; inform and in-form; resign and re-sign; godown and go-down.
The meaning of a word and sound may remain unchanged but people often adopt different styles of spelling representation. The following words largely mean the same thing but the spellings are represented differently by different people:
St. Pete 6393
St. Peter 63930
St. Peters 639306
Saint Pete 61393
Saint Peter 613930
Saint Peters 6139306
Playing games
The ABZZ Code’s thesaurus can be used as a game. Families, groups, or friends travelling together can play challenge games on the ability to generate as many words as possible coding for example, the number plate of the car ahead, or any other number in sight.
This can be fun and a good form of mental athletics among friends.
ABZZ Puzzles
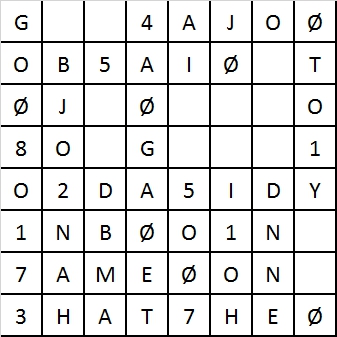
The ABZZ can be used to create mental training alpha-numeric puzzles. In the puzzle below, the first and last names of the 5 last British prime ministers can be found by substituting the numbers with appropriate ABZZ letter equivalents. The symbol “Ø” stands for zero to distinguish it from the alphabet “O”. The answers to the puzzle are presented in the next page.
Mental functions examined would include the ability to remember the ABZZ number and letter equivalents, the names of the last 5 British Prime ministers, and the ability to do the mental substitutions with adequate attentional resources.
Crossword puzzle using the ABZZ code
Name the 5 British Prime Ministers hidden in this alpha-numeric puzzle?
How many can you find?
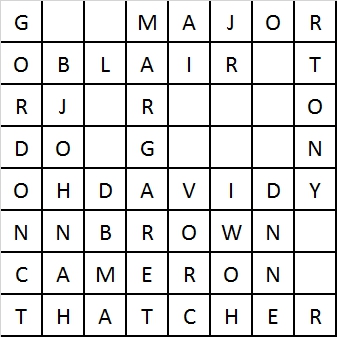
Answer:
Margaret Thatcher
John Major
Tony Blair
Gordon Brown
David Cameron